选课中心
7099人选课
GMAT公开讲座
0元
GRE公开讲座
0元
一对一体验课
99元
GMAT模考网站
10000人
GRE模考网站
GMAT课程
GRE课程
托福辅导课程
【定制】1v1
私人订制
资料下载
考前冲刺
扫码添加助教
免费领取
备考资料大礼包
扫码关注公众号
作为中国考生，本应对数学考试十分自信，但有不少学员反馈，在日常复习和模拟考试的过程中，结果并不太满意，不要说满分，拿高分也不是容易的事。原因是GRE的容错率低，GMAT的出题非常巧妙。
来源：广州新东方 黄楠
我们先来看第一个常见知识点，奇偶性的考察。首先看一道题目：
If x and y are integers and x²y is a positive odd integer, which of the following must be true?
Ⅰ. xy is positive.
Ⅱ. xy is odd.
Ⅲ. x + y is even.
(A) Ⅰ only
(B) Ⅱ only
(C) Ⅲ only
(D) Ⅰ and Ⅱ
(E) Ⅱ and Ⅲ
同学们算出答案了吗?
在解释之前我们先明确 [数字奇偶性]的定义和他们的通项表达式：
偶数： 能够被2整除的整数。
奇数： 不能被2整除的整数。
注意： 奇数和偶数都是交错出现的整数，0是一个特殊的偶数。它既是正偶数与负偶数的分界线，又是正奇数与负奇数的分界线。
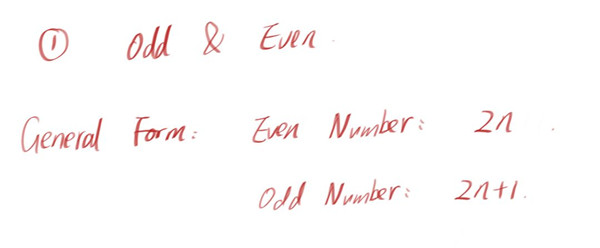
在这个基础上，我们再复习下数字计算的奇偶性：
加法的推导如下：
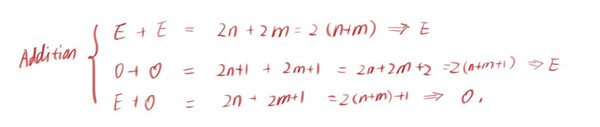
总结如下：凡是同性数字相加，和都是偶数;异性数字相加，和都是奇数。
乘法的推到如下：
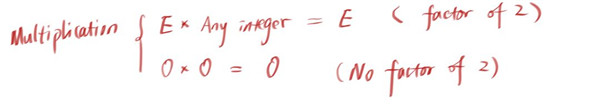
总结如下：凡是有偶数参与的乘法运算，积都是偶数;凡是有奇数参与的乘法运算，积都是奇数。
接下来我们看看题目解析：
我们把x²和y看作两个整数，他们的乘积为奇数，根据上面的乘法法则，推出这两个数字都是奇数。
若x²是奇数，再次根据乘法法则，说明x也是奇数(只有两个奇数相乘，才为奇数)
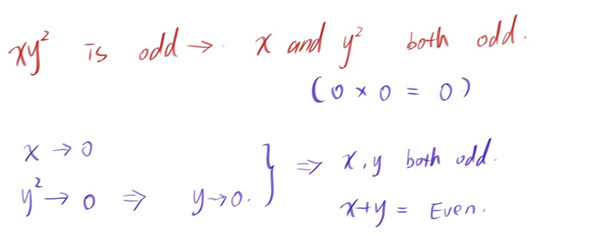
综上，y=positive odd integer; x=odd integer, 由此可得E为正确选项。
接着，我们来看第二个知识点[质因数]prime factor。
同样，先来做一道题目：
If x is the product of the positive integers from 1 to 8, inclusive, and if i, k, m, and p are positive integers such that , then i + k + m + p =
A. 4
B. 7
C. 8
D. 11
E. 12
什么是[质因数]prime factor?
定义：一个整数的质数因数，即为质因数。
那么，我们又先复习 [质数]prime number的概念:
只能被1和它本身整除的数，叫做质数。
注意：
1不是质数(不能分解成1和它本身)，最小质数是2，并且2是唯一的偶数质数。
大于1的任意自然数，要么本身是质数，要么可以分解为几个质数之积(分解质因数)，且这种分解是唯一的。(初等数学基本定理)
熟悉30以内的质数：2，3，5，7，11，13，17，19，23，29。
合数(composite number)：除了1和本身以外，还能被其他整数整除的数字。
注意：
最小合数是4。
所有大于2的偶数都是合数。
奇数也可以是合数(9，15)
综上，我们发现一个结论，数字的奇偶性与质数/合数没有任何关系。即一个奇数，既可以是质数，也可以是合数，偶数亦然。
所以这道题目的解释是：8的阶乘分阶质因数即可。
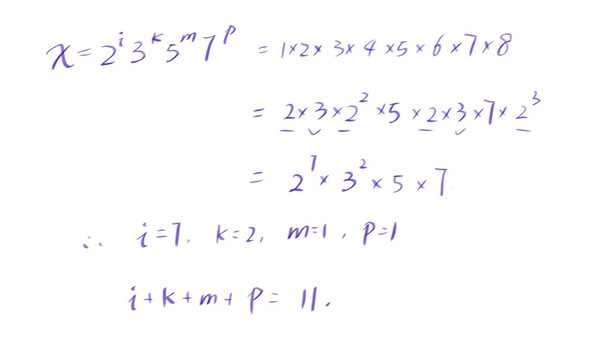
最后我们来看一道这两个知识点的综合题目：
If n and k are integers whose product is 400, which of the following statements must be true?
A. n + k > 0
B. n is not equal to k.
C. Either n or k is a multiple of 10.
D. If n is even, then k is odd.
E. If n is odd, then k is even.
题目解析：
我们一个个排除。
A. 根据负负得正，两个数字都为负数，乘积仍然可以400，故错误。
B. n=k=20, 成绩仍然为400，故错误。
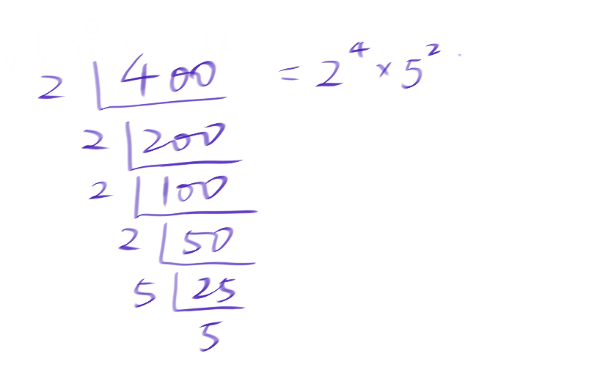
C. 如图所示，分解质因数，n=16, k=25, 两个数字都不是10的倍数。故错误。
D.若n是偶数，我们可以留一个2给后面的k, 导致k也是偶数。故错误。
E. 只剩下这一个选项了。若n是奇数(n没有2作为因数)，2只能留给k，则k一定是偶数。
2月GMAT公益1元公益课【抢报】
资料下载
新东方GMAT佛脚词汇1.0版本
发布时间：2023-06-30添加新东方美研助教号
回复【资料】获取
新东方GMAT数学500题资料下载
发布时间：2023-05-26添加新东方美研助教号
回复【资料】获取
新东方GMAT800题资料下载
发布时间：2022-05-21添加新东方美研助教号
回复【资料】获取
1000句GMAT真实句子改错问题
发布时间：2022-04-17添加新东方美研助教号
回复【资料】获取
2024杨鹏阅读难句（GMAT+GRE）教程
发布时间：2022-04-17添加新东方美研助教号
回复【资料】获取
新东方GMAT数学500题（解析及答案）
发布时间：2019-11-27添加新东方美研助教号
回复【资料】获取
新东方GMAT800题（逻辑+语法+阅读）
发布时间：2019-11-27添加新东方美研助教号
回复【资料】获取
新东方GMAT佛脚词汇1.0版本
发布时间：2019-11-27添加新东方美研助教号
回复【资料】获取
GMAT词汇/长难句/语法资料大全
发布时间：2019-11-27添加新东方美研助教号
回复【资料】获取
GMAT语文考试圣经（Bible）电子版
发布时间：2019-11-27关注新东方在线美研订阅号
回复【GMAT】获取
GMAT推理圣经PDF电子版
发布时间：2019-11-27添加新东方美研助教号
回复【资料】获取
GMAT考试OG五个版本题号对照表
发布时间：2019-11-27添加新东方美研助教号
回复【资料】获取
GMAT Ultimate Grammar电子书籍PDF
发布时间：2019-11-27添加新东方美研助教号
回复【资料】获取
添加美研助教号，
回复【GMAT】获取备考必看资料包
推荐阅读
新东方在线GMAT频道为大家带来GMAT数学答题注意点，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! 1、度量单位
新东方在线GMAT频道为大家带来GMAT数学专用词汇，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! Absolute val
新东方在线GMAT频道为大家带来GMAT数学怎么冲刺满分，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! 1 不要老
新东方在线GMAT频道为大家带来GMAT数学如何获得高分，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! 1 先花一
新东方在线GMAT频道为大家带来GMAT数学基础差怎么办，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! FF宝典和C
新东方在线GMAT频道为大家带来GMAT数学数据填充的要点，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! 1,无需
新东方在线GMAT频道为大家带来GMAT数学的备考习惯，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! 1 不要老是
新东方在线GMAT频道为大家带来GMAT数学具体的备考步骤，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! 首先，
新东方在线GMAT频道为大家带来GMAT数学求余数的复习，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! mod：模。
新东方在线GMAT频道为大家带来GMAT数学成绩怎么快速提升，希望对大家GMAT备考有所帮助。更多精彩尽请关注新东方在线GMAT频道! gmat
资料下载
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
关注新东方在线美研订阅号
回复【GMAT】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
添加新东方美研助教号
回复【资料】获取
阅读排行榜
相关内容
京ICP证050421号 京ICP备05067669号 京公网安备11010802017616号 网络视听许可证0110531号 京网文(2016)1303-163号
Copyright © 2011- 新东方教育科技集团有限公司, All Rights Reserved
优选好课
网友热搜